During all kinds of sports competitions, static data passes on the tv screen. If we look at football, we see, for example, the percentage of possession that a team had until that moment, how many times they shot at the goal and how often that was successful. After a match, much more data is available.
Sports statistics can be used to predicting the outcome of a sports match what you want to bet on. They can give you an indication of the possible outcome. There are two mathematical methods that are often used and that are easy to follow even for a non-mathematician: the binomial and the Poisson distribution.
The two divisions
Given the data available today, both methods are quite useful. The binomial distribution requires more data than the Poisson distribution.
With a binomial distribution, you calculate the probability of success based on a known number of events and a known probability of success per event. Translated into football, that could be: the number of shots on goal (gebnzdg) and the number of goals scored (success).
The Poisson distribution calculates the probability of the average value of something occurring. So you use this distribution when gebnztenisenen gebnzden independently of each other with a known average.
As already mentioned, both methods can be used. In practice, most people choose the Poisson distribution because it is simpler.
Poisson distribution
The Poisson distribution was devised by the French mathematician Siméon Poisson . He was born in 1781, contributed a lot to Applied Mathematics and died at the age of 59. He still had a lot of ideas then. They were later developed by others.
Only the division we are discussing here is named after him. Distribution is a term from probability theory or probability theory. It's called distribution because you calculate how the odds are distributed, for example, the ratio of success to bad luck.
Mathematics can not do without deterring laymen with formulas. That of the Poisson distribution is: P (x; μ) = (e-μ) (μx) / x!
But we will not be deterred by it. Because there are calculators that can perform the calculation. And as you will see, you have enough of a few practical examples to apply the knowledge of this post.
PSV, Feijenoord, Ajax ...
Let's start with a simple example. For convenience, I take PSV, the winner of the 2017-2018 season of the eredivisie. You can then perform it yourself for your own favorite club.
After playing 34 games in that season, PSV had scored a total of 87 goals. That means they averaged 87/34 goals, so 2,294 goal per game.
We leave this average on the formula of the Poisson distribution. Then we see that the probability of PSV not scoring in a match is 10%. The remaining chances are 1 goal 23.1%, 2 goals 26.5%, 3 goals 20.2% and the chance is 11.6% on 4 goals.
Football results
To predict the outcome of a football match, you need that chance of scoring a goal from more clubs. In doing so, we make a distinction between goals in home and away games. And after that we need to relate them to each other in a certain way. We do this by comparing the attacking and defensive strength of clubs.
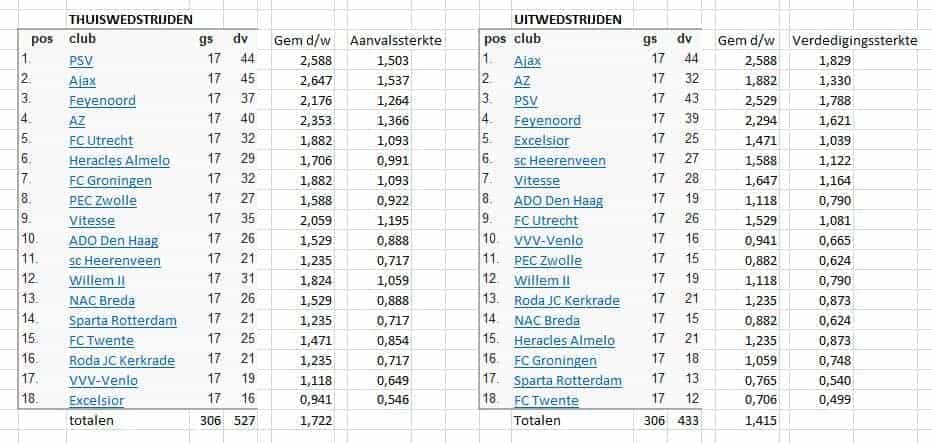
Obviously, it is important to have a representative number of data. With the data of a few matches you can do little. But a football season is enough here. And that data is available everywhere, so we don't have to collect it ourselves. below you can see the data I extracted from wikipedia and processed in a spreadsheet ).
Totals in a season
For the attacking and defensive strength of a club, we first calculate the average goals per game of all clubs combined. We distinguish between home and away goals.
306 matches were played in the 2017-2018 season. You can, of course, calculate that, but that has already been done on various sites. A total of 527 goals were scored by the 18 clubs of the eredivisie in home games and 433 times during away games.
The averages we can calculate from that are:
527 divided by 306 is 1,722 goals in home games and 433 divided by 306 is 1,415 goals in away games. We'll call that the competitive strength here.
Attack and defense strength
The attacking and defensive strength of a club is the ratio of the club average (actually the average number of goals scored by a club) to the league average strength just calculated. For attack strength we look at home games and for defense strength we look at away games.
We calculated the club average of PSV above (by the way, without taking into account away and home games). Let's take Ajax and Heracles.
Ajax's Club average is 2,647 goals from home games and 2,588 goals from away games. That makes 1,537 the attacking strength of Ajax (club average/league strength = 2,647 / 1,722). And the defense strength 1,829 (2,588 / 1,415).
Heracles ' Club average from home games is 1,706 and From Away games 1,235 goals. That makes the attack strength similarly calculated 0.991 (1.706 / 1.772) and the defense strength 0.873 (1.235 / 1.415).
A first prediction
We can now make a first prediction about Ajax's chances of scoring in a home game against Heracles. To do this, we multiply the attacking strength of Ajax by the defensive strength of Heracles and by the competitive strength of home games.
So: 1,537 x 0,873 x 1,722 = 2,310 goals
Conversely, we can calculate the scoring chances of Heracles by their attacking strength against AJAX's defensive strength and the competition strength of away games.
So: 0,991 x 1,829 x 1,415 = 2,564 goals
One would say at first glance that the match has a great chance of ending in a draw. However, we cannot use a result of 2.3 against 2.5. They are only averages, even though we already know by this result that we are probably going to put a cross on a draw.

The probability that Ajax does not score is therefore almost 10%. The probability that they score 2 times is greatest with 26.48%. That Heracles scores 2 times is also the greatest with them. Thus, it is clear that the probability of a draw (2 -2 ) is the greatest.
Probability distribution
In the above example, it can be seen quite quickly that the mentioned probability of a result (2-2) is the greatest. By multiplying percentages you can see the actual odds for every score imaginable.
- The probability of 0-0 is 0.0992 x 0.0770 = 0.0076 = 0.7%
- The probability of 3-3-is 0.2039 x 0.2163 = 4.4%
- The probability of 1-2 is 0.2292 x 0.1974 = 4.5%
- The probability of 2-2 is 0.2648 x 0.2530 = 6.6%
- The probability of 2-1 is 0.2648 x 0.1974 = 5.2%
- Etc.
This can be useful when you want to make a comparison with the percentages of bookmakers. At our highest football competition, it turns out that, apart from disappointing play, the scoring chances of clubs are close to each other. For example, See also the additional example below.
Abroad and in other sports, they are further apart. And now that you know the principle of the poisson distribution, you may also be able to use it in other sports or in completely different situations. For example, it is also used when calculating error rates, collisions, bird counts, etc.
An additional example
An additional example shows the scoring percentages of the match VVV Venlo – Ajax.
VVV Venlo averaged 1,118 goals at home and 0,941 away. With that, it has an attack strength of 0.366 and a defense strength of 0.469 goals.
The scoring chances of VVV Venlo (the home-playing club) thus become 1.15 goals. Ajax scored 1.02 goals. Note that you have to recalculate Ajax's figures for the match against VVV Venlo; they are not the same as with Heracles.
Thus, the match VVV Venlo – Ajax looks like this:

Finally
The Poisson distribution helps you make an estimate of a sports result or result, for example: betting on football . However, there are many factors that you have no influence on and that are not taken into account in the calculation. The weather, the purchase of a new striker, a grumpy trainer, wearing new shoes and more.
You take the influence of that kind of data into account when assessing a forecast. Before that, you read sports magazines, watch sports programs and listen to friends. Some data can also be put back into a Poisson distribution; for example, the goal scoring average of the new striker. But in the end, of course, every match remains a game of chance.
Calculators
There are several calculators for calculating the poisson distribution. For example, on EasyCalculation and Free Statistics Caculator .
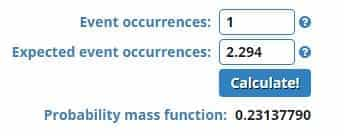
To illustrate the above example of PSV, the probability of 23.1% on 1 goal.
So at the bottom of the found average and at the top always make a recalculation. Pay attention to the point (.) for decimals.
Source:
For the above post, I used old school wisdom. More information can be found on the internet if you want to delve further into Poisson distribution and other (probability)calculation methods. This English project report is specifically about predicting football results, among other things with Poisson distribution in the manner described above.
And the promised spreadsheet about Season 2017-2018: